If b is very small as compared to the value of a, so that the cube and other higher powers of $\frac{b}{a}$ can be neglected in the identity
$\frac{1}{a-b}+\frac{1}{a-2 b}+\frac{1}{a-3 b}+\ldots .+\frac{1}{a-n b}=\alpha n+\beta n^{2}+\gamma n^{3}$
then the value of $\gamma$ is :
Correct Option: , 4
$\frac{\mathrm{dy}-\mathrm{dx}}{\mathrm{e}^{\mathrm{y}-\mathrm{x}}}=\mathrm{x} \mathrm{dx}$
$\Rightarrow \frac{d y-d x}{e^{y-x}}=x d x$
$\Rightarrow-e^{x-y}=\frac{x^{2}}{2}+c$
At $x=0, y=0 \Rightarrow c=-1$
$\Rightarrow e^{x-y}=\frac{2-x^{2}}{2}$
$\Rightarrow y=x-\ell n\left(\frac{2-x^{2}}{2}\right)$
$\Rightarrow \frac{d y}{d x}=1+\frac{2 x}{2-x^{2}}=\frac{2+2 x-x^{2}}{2-x^{2}}$
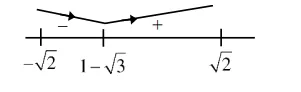
So minimum value occurs at $x=1-\sqrt{3}$
$y(1-\sqrt{3})=(1-\sqrt{3})-\ell n\left(\frac{2-(4-2 \sqrt{3})}{2}\right)$
$=(1-\sqrt{3})-\ell \mathrm{n}(\sqrt{3}-1)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.