Question.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
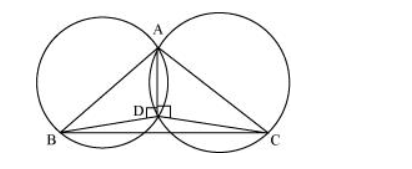
Consider a $\triangle \mathrm{ABC}$.
Two circles are drawn while taking $A B$ and $A C$ as the diameter.
Let they intersect each other at $D$ and let $D$ not lie on $B C$.
Join AD.
$\angle A D B=90^{\circ}$ (Angle subtended by semi-circle)
$\angle \mathrm{ADC}=90^{\circ}$ (Angle subtended by semi-circle)
$\angle B D C=\angle A D B+\angle A D C=90^{\circ}+90^{\circ}=180^{\circ}$
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point $D$ lies on third side $B C$ of $\triangle A B C$.
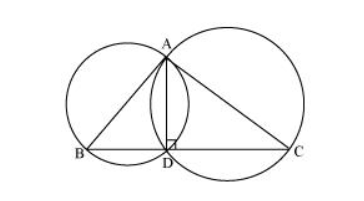
Consider a $\triangle \mathrm{ABC}$.
Two circles are drawn while taking $A B$ and $A C$ as the diameter.
Let they intersect each other at $D$ and let $D$ not lie on $B C$.
Join AD.
$\angle A D B=90^{\circ}$ (Angle subtended by semi-circle)
$\angle \mathrm{ADC}=90^{\circ}$ (Angle subtended by semi-circle)
$\angle B D C=\angle A D B+\angle A D C=90^{\circ}+90^{\circ}=180^{\circ}$
Therefore, BDC is a straight line and hence, our assumption was wrong.
Thus, Point $D$ lies on third side $B C$ of $\triangle A B C$.