If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral,
Question.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
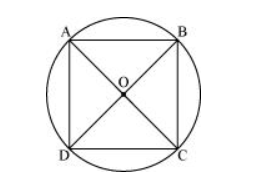
Let $A B C D$ be a cyclic quadrilateral having diagonals $B D$ and $A C$, intersecting each other at point $O$.
$\angle B A D=\frac{1}{2} \angle B O D=\frac{180^{\circ}}{2}=90^{\circ}$ (Consider BD as a chord)
$\angle B C D+\angle B A D=180^{\circ}($ Cyclic quadrilateral $)$
$\angle B C D=180^{\circ}-90^{\circ}=90^{\circ}$
$\angle \mathrm{ADC}=\frac{1}{2} \angle \mathrm{AOC}=\frac{1}{2}\left(180^{\circ}\right)=90^{\circ}(\mathrm{Considering} \mathrm{AC}$ as a chord $)$
$\angle A D C+\angle A B C=180^{\circ}$ (Cyclic quadrilateral)
$90^{\circ}+\angle A B C=180^{\circ}$
$\angle A B C=90^{\circ}$
Each interior angle of a cyclic quadrilateral is of 90°. Hence, it is a rectangle.
Let $A B C D$ be a cyclic quadrilateral having diagonals $B D$ and $A C$, intersecting each other at point $O$.
$\angle B A D=\frac{1}{2} \angle B O D=\frac{180^{\circ}}{2}=90^{\circ}$ (Consider BD as a chord)
$\angle B C D+\angle B A D=180^{\circ}($ Cyclic quadrilateral $)$
$\angle B C D=180^{\circ}-90^{\circ}=90^{\circ}$
$\angle \mathrm{ADC}=\frac{1}{2} \angle \mathrm{AOC}=\frac{1}{2}\left(180^{\circ}\right)=90^{\circ}(\mathrm{Considering} \mathrm{AC}$ as a chord $)$
$\angle A D C+\angle A B C=180^{\circ}$ (Cyclic quadrilateral)
$90^{\circ}+\angle A B C=180^{\circ}$
$\angle A B C=90^{\circ}$
Each interior angle of a cyclic quadrilateral is of 90°. Hence, it is a rectangle.