If from an external point B of a circle with centre 0,

Two tangents BD and BC are drawn from an external point B.

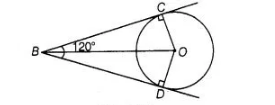
To prove $\quad B O=2 B C$

Given, $\angle D B C=120^{\circ}$

Join $O C, O D$ and $B O$.

Since, $B C$ and $B D$ are tangents.

$\therefore \quad O C \perp B C$ and $O D \perp B D$

We know, $O B$ is a angle bisector of $\angle D B C$.

$\therefore$ $\angle O B C=\angle D B O=60^{\circ}$

In right angled $\triangle O B C$, $\cos 60^{\circ}=\frac{B C}{O B}$

$\Rightarrow$ $\frac{1}{2}=\frac{B C}{O B}$

$\Rightarrow$ $O B=2 B C$

Also, $B C=B D$

[tangent drawn from internal point to circle are equal]

$\therefore$ $O B=B C+B C$

$\Rightarrow$ $O B=B C+B D$