If $n(A)=3$ and $n(B)=5$, find:
(i) The maximum number of elements in $A \cup B$,
(ii) The minimum number of elements in $A \cup B$.
Number of elements in set A n(A) = 3 and number of elements in set B n(B) =
5
The number of elements in $A \cup B$ is $n(A \cup B)$.
i) Now for elements in $\mathrm{A} \cup \mathrm{B}$ to be maximum, there should not be any intersection between both sets that is $A$ and $B$ both sets must be disjoint sets as shown.
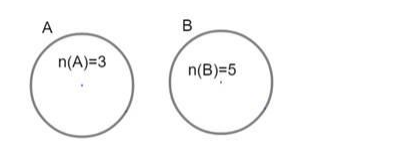
Hence the number of elements in $A \cup B$ is $n(A \cup B)=n(A)+n(B)$
$\Rightarrow \mathrm{n}(\mathrm{A} \cup \mathrm{B})=3+5$
$\Rightarrow \mathrm{n}(\mathrm{A} \cup \mathrm{B})=8$
Hence maximum number of elements in $A \cup B$ is 8
ii) Now for a number of elements in $\mathrm{A} \cup \mathrm{B}$ to be minimum, there should be an ntersection between sets $A$ and $B$ so that some elements are common
The count will be minimum when all the elements from set $A$ are also in set $B$ the reverse are not possible because $n(A) Hence if the 3 elements of $A$ are in the intersection of $A$ and $B$, then the number of elements only in $B$ will be 2 because $n(B)=5$ Visually it is represented as As seen from the figure the number of elements in $A \cup B$ is 5 hence minimum number of elements in $A \cup B=5$ 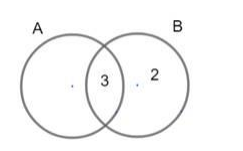
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
