If PA and PB are tangents from an outside point P such

Let us first put the given data in the form of a diagram.

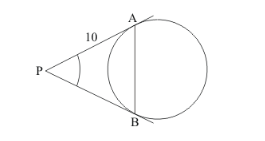
From the property of tangents we know that the length of two tangents drawn to a circle from a common external point will always be equal. Therefore,

PA=PB

Consider the triangle PAB. Since we have PA=PB, it is an isosceles triangle. We know that in an isosceles triangle, the angles opposite to the equal sides will be equal. Therefore we have,

Also, sum of all angles of a triangle will be equal to . Therefore,

$\angle P A B+\angle P B A+\angle A P B=180^{\circ}$

$60^{\circ}+2 \angle P B A=180^{\circ}$

$2 \angle P B A=120^{\circ}$

$\angle P A B=60^{\circ}$

Since we know that $\angle P A B=\angle P B A$,

$\angle P A B=60^{\circ}$

Now if we see the values of all the angles of the triangle, all the angles measure. Therefore triangle PAB is an equilateral triangle.

We know that in an equilateral triangle all the sides will be equal.

It is given in the problem that side PA = 10 cm. Therefore, all the sides will measure 10 cm. Hence, AB = 10 cm.

Thus the length of the chord AB is 10 cm.