If radii of two concentric circles are 4 cm and 5 cm,

(b) Let 0 be the centre of two concentric circles C1 and C2, whose radii are r1 = 4 cm and r2 = 5 cm. Now, we draw a chord AC of circle C2, which

touches the circle C1 at B.

Also, join OB, which is perpendicular to AC. [Tangent at any point of circle is perpendicular to radius throughly the point of contact]

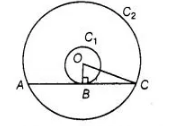
Now, in right angled $\triangle O B C$, by using Pythagoras theorem,

$O C^{2}=B C^{2}+B O^{2}$

$\left[\because(\text { hypotenuse })^{2}=(\text { base })^{2}+(\text { perpendicular })^{2}\right]$

$\Rightarrow \quad 5^{2}=B C^{2}+4^{2}$

$\Rightarrow \quad B C^{2}=25-16=9 \Rightarrow B C=3 \mathrm{~cm}$

$\therefore \quad$ Length of chord $A C=2 B C=2 \times 3=6 \mathrm{~cm}$