If $\sin A=\frac{9}{41}$, compute $\cos A$ and $\tan A$.
Given: $\sin A=\frac{9}{41}$...(1)
To Find: $\cos A, \tan A$
By definition,
$\sin A=\frac{\text { Perpendicular side opposite to } \angle \mathrm{A}}{\text { Hypotenuse }}$…... (2)
By Comparing (1) and (2)
We get,
Perpendicular side = 9 and
Hypotenuse = 41
Now using the perpendicular side and hypotenuse we can construct $\triangle A B C$ as shown below
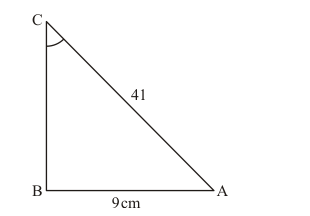
Length of side $\mathrm{AB}$ is unknown in right angled $\triangle A B C$,
To find length of side AB, we use Pythagoras theorem.
Therefore, by applying Pythagoras theorem in $\triangle A B C$,
We get,
$A C^{2}=A B^{2}+B C^{2}$
$41^{2}=A B^{2}+9^{2}$
$A B^{2}=41^{2}-9^{2}$
$A B^{2}=1681-81$
$A B^{2}=1600$
$A B=\sqrt{1600}$
$A B=40$
Hence, length of side AB = 40
Now,
By definition,
$\cos A=\frac{\text { Base side adjacent to } \angle \mathrm{A}}{\text { Hypotenuse }}$
$\cos A=\frac{A B}{\mathrm{AC}}$
$\cos A=\frac{40}{41}$
Now,
By definition,
$\tan A=\frac{\text { Perpendicular side opposite to } \angle \mathrm{A}}{\text { Base side adjacent to } \angle \mathrm{A}}$
$\tan A=\frac{B C}{\mathrm{AB}}$
$\tan A=\frac{9}{40}$
Answer: $\cos A=\frac{40}{41}$ and $\tan A=\frac{9}{40}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
