If tan θ=2021, show that 1−sin θ+cos θ1+sin θ+cos θ=37.

Given:

$\tan \theta=\frac{20}{21}$.....(1)

To show that:

$\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}=\frac{3}{7}$

Now we know $\tan \theta$ is defined as follows

$\tan \theta=\frac{\text { Perpendicular side opposite to } \angle \theta}{\text { Base side adjacent to } \angle \theta}$....(2)

Now by comparing equation (1) and (2)

We get

Perpendicular side opposite to $\angle \theta=20$

Base side adjacent to $\angle \theta=21$

Therefore triangle representing angle $\theta$ is as shown below

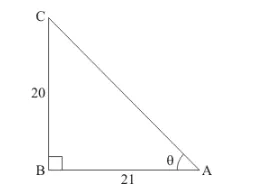
Side AC is unknown and can be found using Pythagoras theorem

Therefore,

$A C^{2}=A B^{2}+B C^{2}$Now by substituting the value of known sides from figure (a)

We get,

$A C^{2}=21^{2}+20^{2}$

$=441+400$

$=841$

Now by taking square root on both sides

We get,

$A C=\sqrt{841}$

$=29$

Therefore Hypotenuse side AC = 29 …… (3)

Now we know, $\sin \theta$ is defined as follows

$\sin \theta=\frac{\text { Perpendicular side opposite to } \angle \theta}{\text { Hypotenuse }}$

Therefore from figure (a) and equation (3)

We get,

$\sin \theta=\frac{B C}{A C}$

$=\frac{20}{29}$

$\sin \theta=\frac{20}{29} \ldots \ldots$(4)

Now we know, $\cos \theta$ is defined as follows

$\cos \theta=\frac{\text { Base side adjacent to } \angle \theta}{\text { Hypotenuse }}$

Therefore from figure (a) and equation (3)

We get,

$\cos \theta=\frac{A B}{A C}$

$=\frac{21}{29}$

$\cos \theta=\frac{21}{29}$....(5)

Now we need to find the value of expression $\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}$

Therefore by substituting the value of $\sin \theta$ and $\cos \theta$ from equation (4) and (5) respectively, we get,

$\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}=\frac{1-\frac{20}{29}+\frac{21}{29}}{1+\frac{20}{29}+\frac{21}{29}}$

Now by taking L.C.M on R.H.S of above equation

We get

$\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}=\frac{\frac{29-20+21}{29}}{\frac{29+20+21}{29}}$

$=\frac{\frac{29+1}{29}}{\frac{70}{29}}$

$=\frac{\frac{30}{29}}{\frac{70}{29}}$

$=\frac{30}{29} \times \frac{29}{70}$

$=\frac{30}{70}$

$=\frac{3 \times 10}{7 \times 10}$

Now as 10 is present in numerator as well as denominator of R.H.S of above equation, it gets cancelled and we get

$\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}=\frac{3}{7}$

Hence $\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}=\frac{3}{7}$