If the adjoining figure is a sector of a circle of radius 10.5 cm,

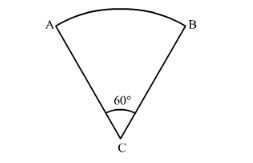
Given figure is a quadrant of a circle. We have given radius of sector that is 10.5 cm. Arc AB subtended an angle of 60° at the centre of the circle.

Perimeter of the sector $=\frac{\theta}{360} \times 2 \pi r+2 r$

Substituting the values we get,

Perimeter of the sector $=\frac{60}{360} \times 2 \pi \times 10.5+2 \times 10.5$

Now we will simplify equation (1) as shown below,

Perimeter of the sector $=\frac{1}{6} \times 2 \pi \times 10.5+2 \times 10.5$

Perimeter of the sector $=\frac{1}{6} \times 21 \pi+21$

Now we will substitute $\pi=\frac{22}{7}$.

Perimeter of the sector $=\frac{1}{6} \times 21 \times \frac{22}{7}+21$

Perimeter of the sector $=\frac{1}{6} \times 3 \times 22+21$

Perimeter of the sector $=11+21$

Perimeter of the sector $=32$

Therefore, perimeter of the given sector is $32 \mathrm{~cm}$.