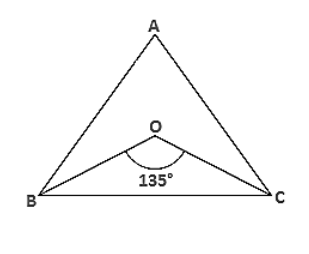
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right angle.

Given the bisectors of the base angles of a triangle enclose an angle of $135^{\circ}$

i.e., $\angle B O C=135^{\circ}$

But, We know that

$\angle \mathrm{BOC}=90^{\circ}+\frac{1}{2} \angle \mathrm{A}$

$\Rightarrow 135^{\circ}=90^{\circ}+\frac{1}{2} \angle \mathrm{A}$

$\Rightarrow \frac{1}{2} \angle \mathrm{A}=135^{\circ}-90^{\circ}$

⇒ ∠A = 45°(2)

⇒ ∠A = 90°

Therefore, ΔABC is a right angle triangle that is right angled at A.