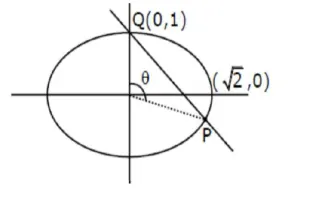
If the curve $x^{2}+2 y^{2}=2$ intersects the line $x+y=1$ at two points $P$ and $Q$, then the angle subtended by the line segment $\mathrm{PQ}$ at the origin is:
Correct Option: 1,
Ellipse $\frac{x^{2}}{2}+\frac{y^{2}}{1}=1$
Line $x+y=1$
Using homogenisation $x^{2}+2 y^{2}=2(1)^{2}$
$x^{2}+2 y^{2}=2(x+y)^{2}$
$x^{2}+2 y^{2}=2 x^{2}+2 y^{2}+4 x y$
$x^{2}+4 x y=0$
for $a x^{2}+2 h x y+b y^{2}=0$
$\tan \theta=\left|\frac{2 \sqrt{h^{2}-a b}}{a+b}\right|$
$\tan \theta=\left|\frac{2 \sqrt{(2)^{2}-0}}{1+0}\right|$
$\tan \theta=-4$
$\cot \theta=-\frac{1}{4}$
$\theta=\cot ^{-1}\left(-\frac{1}{4}\right)$
$\theta=\pi-\cot ^{-1}\left(\frac{1}{4}\right)$
$\theta=\pi-\left(\frac{\pi}{2}-\tan ^{-1}\left(\frac{1}{4}\right)\right)$
$\theta=\frac{\pi}{2}+\tan ^{-1}\left(\frac{1}{4}\right)$
