If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Solution:



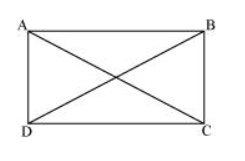
Let $A B C D$ be a parallelogram. To show that $A B C D$ is a rectangle, we have to prove that one of its interior angles is $90^{\circ}$.

In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DCB}$

$A B=D C$ (Opposite sides of a parallelogram are equal)

$\mathrm{BC}=\mathrm{BC}$ (Common)

$\mathrm{AC}=\mathrm{DB}$ (Given)

$\therefore \triangle \mathrm{ABC} \cong \triangle \mathrm{DCB}$ (By SSS Congruence rule)

$\Rightarrow \angle \mathrm{ABC}=\angle \mathrm{DCB}$

It is known that the sum of the measures of angles on the same side of transversal is $180^{\circ}$.

$\angle \mathrm{ABC}+\angle \mathrm{DCB}=180^{\circ}(\mathrm{AB} \| \mathrm{CD})$

$\Rightarrow \angle \mathrm{ABC}+\angle \mathrm{ABC}=180^{\circ}$

$\Rightarrow 2 \angle \mathrm{ABC}=180^{\circ}$

$\Rightarrow \angle \mathrm{ABC}=90^{\circ}$

Since $A B C D$ is a parallelogram and one of its interior angles is $90^{\circ}, A B C D$ is a rectangle.