Question:
If the diagram in Fig. $2.22$ shows the graph of the polynomial $f(x)=a x^{2}+b x+c$, then
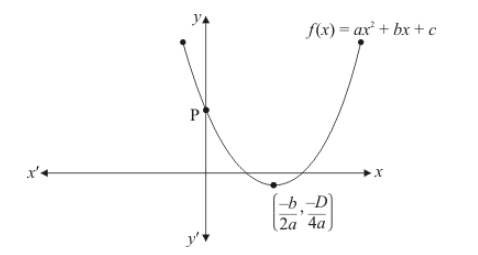
(a) $a>0, b<0$ and $c>0$
(b) $a<0, b<0$ and $c<0$
(c) $a<0, b>0$ and $c>0$
(d) $a<0, b>0$ and $c<0$
Solution:
Clearly, $f(x)=a x^{2}+b x+c$ represent a parabola opening upwards.
Therefore, $a>0 \quad y=a x^{2}+b x+c$ cuts $Y$ axis at $P$ which lies on $O Y$. Putting $x=0$ in $y=a x^{2}+b x+c$, we get $y=c$. So the coordinates of $P$ is $(0, c)$. Clearly, $\mathrm{P}$ lies on $O Y$. Therefore $c>0$
Hence, the correct choice is $(a)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
