If the equation of the base of an equilateral

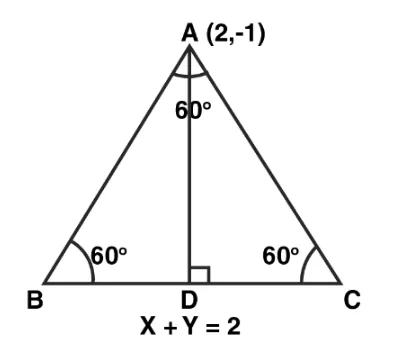
Let $\triangle \mathrm{ABC}$ be an equilateral triangle.

Given equation of the base $B C$ is $x+y=2$

We know that, in an equilateral triangle all angles are of $60^{\circ}$

So, in $\triangle \mathrm{ABD}$

$\sin 60^{\circ}=\frac{\mathrm{AD}}{\mathrm{AB}}$\

$\Rightarrow \frac{\sqrt{3}}{2}=\frac{\mathrm{AD}}{\mathrm{AB}}\left[\because \sin 60^{\circ}=\frac{\sqrt{3}}{2}\right]$

$\Rightarrow \mathrm{AD}=\frac{\sqrt{3}}{2} \mathrm{AB}$

We know that, the distance $d$ of a point $P\left(x_{0}, y_{0}\right)$ from the line $A x+B y+C=0$ is given by

$d=\left|\frac{A x_{0}+B y_{0}+C}{\sqrt{A^{2}+B^{2}}}\right|$

Now, length of perpendicular from vertex $A(2,-1)$ to the line $x+y=2$ is

$\mathrm{AD}=\left|\frac{1 \times 2+1 \times(-1)-2}{\sqrt{(1)^{2}+(1)^{2}}}\right|$

$\Rightarrow \frac{\sqrt{3}}{2} \mathrm{AB}=\left|\frac{2-1-2}{\sqrt{2}}\right|$

On simplification we get

$\Rightarrow \frac{\sqrt{3}}{2} \mathrm{AB}=\frac{1}{\sqrt{2}}$

Squaring both the sides, we get

$\Rightarrow \frac{3}{4} \mathrm{AB}^{2}=\frac{1}{2}$

On cross multiplication we get

$\Rightarrow \mathrm{AB}^{2}=\frac{4}{3} \times \frac{1}{2}$

$\Rightarrow \mathrm{AB}^{2}=\frac{2}{3}$

$\Rightarrow A B=\sqrt{\frac{2}{3}}$

Hence, the required length of side is $\sqrt{\frac{2}{3}}$