If the figure below forms a linear pair,
∠EOB = ∠FOC = 90 and ∠DOC = ∠FOG = ∠AOB = 30
Find the measure of ∠FOE, ∠COB and ∠DOE
Name all the right angles
Name three pairs of adjacent complementary angles
Name three pairs of adjacent supplementary angles
Name three pairs of adjacent angles
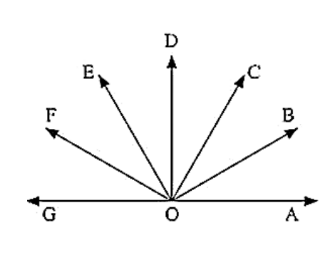
(i) ∠FOE = x, ∠DOE = y and ∠BOC = z
Since ∠AOF, ∠FOG is a linear pair
∠AOF + 30 = 180
∠AOF = 180 - 30
∠AOF = 150
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF = 150
30 + z + 30 + y + x = 150
x + y + z =150 - 30 - 30
x + y + z = 90 .... (1)
∠FOC = 90°
∠FOE + ∠EOD + ∠DOC = 90°
x + y + 30 = 90
x + y = 90 - 30
x + y =60 ... (2)
Substituting (2) in (1)
x + y + z = 90
60 + z = 90
z = 90 - 60 = 30
Given BOE = 90
∠BOC + ∠COD + ∠DOE = 90°
30 + 30 + DOE = 90
DOE = 90 - 60 = 30
DOE = x = 30
We also know that,
x + y = 60
y = 60 - x
y = 60 - 30
y = 30
Thus we have ∠FOE = 30, ∠COB = 30 and ∠DOE = 30
(ii) Right angles are ∠DOG, ∠COF, ∠BOF, ∠AOD
(iii) Adjacent complementary angles are (∠AOB, ∠BOD); ( ∠AOC, ∠COD); ( ∠BOC, ∠COE)
(iv) Adjacent supplementary angles are (∠AOB, ∠BOG); (∠AOC, ∠COG); (∠AOD, ∠DOG)
(v) Adjacent angles are (∠BOC, ∠COD); (∠COD, ∠DOE); (∠DOE, ∠EOF)