Question:
If the four complex numbers $z, \bar{z}, \bar{z}-2 \operatorname{Re}(\bar{z})$ and $z-2 \operatorname{Re}(z)$ represent the vertices of a square of side 4 units in the Argand plane, then $|z|$ is equal to :
Correct Option: , 3
Solution:
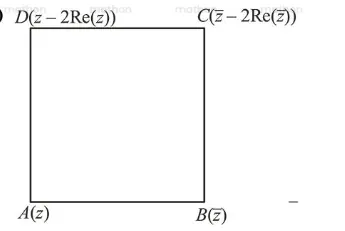
Let $z=x+i y$
$\because$ Length of side of square $=4$ units
Then, $|z-\bar{z}|=4 \Rightarrow|2 i y|=4 \Rightarrow|y|=2$
Also, $|z-(z-2 \operatorname{Re}(z))|=4$
$\Rightarrow|2 \operatorname{Re}(z)|=4 \Rightarrow|2 x|=4 \Rightarrow|x|=2$
$\therefore|z|=\sqrt{x^{2}+y^{2}}=\sqrt{4+4}=2 \sqrt{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.