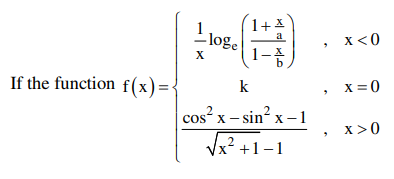
is continuous at $x=0$, then $\frac{1}{a}+\frac{1}{b}+\frac{4}{k}$ is equal to :
Correct Option: 1
If $f(x)$ is continuous at $x=0, R H L=L H L=f(0)$
$\lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{+}} \frac{\cos ^{2} x-\sin ^{2} x-1}{\sqrt{x^{2}+1}-1} \cdot \frac{\sqrt{x^{2}+1}+1}{\sqrt{x^{2}+1}+1}$ (Rationalisation)
$\lim _{x \rightarrow 0^{+}}-\frac{2 \sin ^{2} x}{x^{2}} \cdot\left(\sqrt{x^{2}+1}+1\right)=-4$
$\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{-}} \frac{1}{x} \ell\left(\frac{1+\frac{x}{a}}{1-\frac{x}{b}}\right)$
$\lim _{x \rightarrow 0^{-}} \frac{\ln \left(1+\frac{x}{a}\right)}{\left(\frac{x}{a}\right) \cdot a}+\frac{\ln \left(1-\frac{x}{b}\right)}{\left(-\frac{x}{b}\right) \cdot b}$
$=\frac{1}{a}+\frac{1}{b}$
$\mathrm{So} \frac{1}{\mathrm{a}}+\frac{1}{\mathrm{~b}}=-4=\mathrm{k}$
$\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{4}{k}=-4-1=-5$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
