If the height of a tower and the distance

True

Case I Let the height of a tower be $h$ and the distance of the point of observation from its foot is $x$.

In $\triangle A B C$,

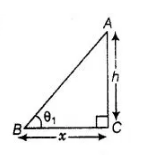
$\tan \theta_{1}=\frac{A C}{B C}=\frac{h}{x}$

$\Rightarrow \quad \theta_{1}=\tan ^{-1}\left(\frac{h}{x}\right)$ $\ldots$ (i)

Case II Now, the height of a tower increased by $10 \%=h+10 \%$ of $h=h+h \times \frac{10}{100}=\frac{11 h}{10}$ and the distance of the point of observation from its foot $=x+10 \%$ of $x$

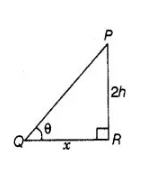
$=x+x \times \frac{10}{100}=\frac{11 x}{10}$

$\ln \triangle P Q R$, $\tan \theta_{2}=\frac{P R}{Q R}=\frac{\left(\frac{11 h}{10}\right)}{\left(\frac{11 x}{10}\right)}$

$\Rightarrow \quad \tan \theta_{2}=\frac{h}{x}$

$\because \quad \theta_{2}=\tan ^{-1}\left(\frac{h}{x}\right)$  .....(ii)

From Eqs. (i) and (ii),

$\theta_{1}=\theta_{2}$

Hence,the required angle of elevation of its top remains unchanged