If the length of the shadow of a tower is increasing,

False

To understand the fact of this question, consider the following example I. A tower $2 \sqrt{3} \mathrm{~m}$ high casts a shadow $2 \mathrm{~m}$ long on the ground, then the Sun's elevation is $60^{\circ}$.

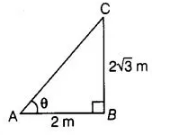
In $\triangle A C B$,  $\tan \theta=\frac{A B}{B C}=\frac{2 \sqrt{3}}{2}$

$\Rightarrow \quad \tan \theta=\sqrt{3}=\tan 60^{\circ}$

$\therefore \quad \theta=60^{\circ}$

II. A same hight of tower casts a shadow $4 \mathrm{~m}$ more from preceding point, then the Sun's elevation is $30^{\circ}$.

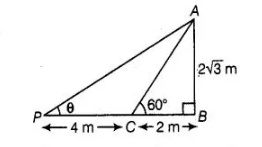
In $\Delta A P B, \quad \tan \theta=\frac{A B}{P B}=\frac{A B}{P C+C B}$

$\Rightarrow$ $\tan \theta=\frac{2 \sqrt{3}}{4+2}=\frac{2 \sqrt{3}}{6}$

$\Rightarrow$ $\tan \theta=\frac{\sqrt{3}}{3} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{3}{3 \sqrt{3}}$

$\Rightarrow$ $\tan \theta=\frac{1}{\sqrt{3}}=\tan 30^{\circ}$

$\therefore \quad \theta=30$

Hence, we conclude from above two examples that if the length of the shadow of a tower is increasing, then the angle of elevation of the Sun is

decreasing.

Alternate Method

False, we know that, if the elevation moves towards the tower, it increases and if its elevation moves away the tower, it decreases. Hence, if the

shadow of a tower is increasing, then the angle of elevation of a Sun is not increasing