Question:
If the line $y=m x$ bisects the area enclosed by the lines $x=0, y=0, x=\frac{3}{2}$ and the curve $y=1+4 x-x^{2}$, then $12 m$ is equal to________.
Solution:
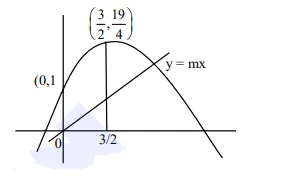
Total area $=\int_{0}^{3 / 2}\left(1+4 x-x^{2}\right) d x$
$=x+2 x^{2}-\left.\frac{x^{3}}{3}\right|_{0} ^{3 / 2}=\frac{39}{8}$
$\& \frac{39}{16}=\frac{1}{2} \cdot \frac{3}{2} \cdot \frac{3}{2} \mathrm{~m}$
$\Rightarrow 3 \mathrm{~m}=\frac{13}{2} \Rightarrow 12 \mathrm{~m}=26$
