If the medians of a AABC intersect at G,

Solution:

Given In ΔABC, AD, BE and CF are medians and intersect at G.

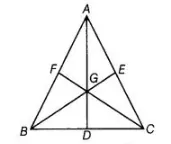
To prove ar $(\Delta A G B)=\operatorname{ar}(\Delta A G C)=\operatorname{ar}(\Delta B G C)=\frac{1}{3} \operatorname{ar}(\Delta A B C)$

Proof We know that, a median of a triangle divides it into two triangles of equal area. In $\triangle A B C, A D$ is a median.

$\therefore \quad a r(\Delta A B D)=\operatorname{ar}(\triangle A C D)$ $\ldots(\mathrm{i})$

In $\triangle B G C, G D$ is a median.

$\therefore \quad a r(\Delta G B D)=\operatorname{ar}(\Delta G C D)$ ....(ii)

On subtracting Eq. (ii) from Eq. (i), we get

$\operatorname{ar}(\Delta A B D)-\operatorname{ar}(\Delta G B D)=\operatorname{ar}(\triangle A C D)-\operatorname{ar}(\Delta G C D)$

$\Rightarrow \quad \operatorname{ar}(\Delta A G B)=\operatorname{ar}(\triangle A G C)$ ....(iii)

Similarly,

$\operatorname{ar}(\Delta A G B)=\operatorname{ar}(\Delta B G C)$

From Eqs. (iii) and (iv).

$\operatorname{ar}(\Delta A G B)=\operatorname{ar}(\Delta B G C)=\operatorname{ar}(\Delta A G C)$ $\ldots(\mathrm{v})$

NOW,

$\operatorname{ar}(\Delta A B C)=\operatorname{ar}(\Delta A G B)+\operatorname{ar}(\Delta B G C)+\operatorname{ar}(\Delta A G C)$

$\Rightarrow \quad \operatorname{ar}(\Delta A B C)=\operatorname{ar}(\Delta A G B)+\operatorname{ar}(\Delta A G B)+\operatorname{ar}(\Delta A G B) \quad$ [from Eq. (v)]

$\Rightarrow \quad \operatorname{ar}(\Delta A B C)=3 \operatorname{ar}(\Delta A G B)$ 

$\Rightarrow \quad \operatorname{ar}(\Delta A G B)=\frac{1}{3} \operatorname{ar}(\Delta A B C)$ $\ldots(\mathrm{vi})$

From Eqs. (v) and (vi),

$\operatorname{ar}(\Delta B G C)=\frac{1}{3} \operatorname{ar}(\Delta A B C)$

and $\operatorname{ar}(\triangle A G C)=\frac{1}{3} \operatorname{ar}(\Delta A B C)$

Hence proved.