If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10)

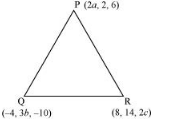
It is known that the coordinates of the centroid of the triangle, whose vertices are $\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)$ and $\left(x_{3}, y_{3}, z_{3}\right)$, are $\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}, \frac{z_{1}+z_{2}+z_{3}}{3}\right)$.

Therefore, coordinates of the centroid of $\triangle \mathrm{PQR}=\left(\frac{2 a-4+8}{3}, \frac{2+3 b+14}{3}, \frac{6-10+2 c}{3}\right)=\left(\frac{2 a+4}{3}, \frac{3 b+16}{3}, \frac{2 c-4}{3}\right)$

It is given that origin is the centroid of ΔPQR.

$\therefore(0,0,0)=\left(\frac{2 a+4}{3}, \frac{3 b+16}{3}, \frac{2 c-4}{3}\right)$

$\Rightarrow \frac{2 a+4}{3}=0, \frac{3 b+16}{3}=0$ and $\frac{2 c-4}{3}=0$

$\Rightarrow a=-2, b=-\frac{16}{3}$ and $c=2$

Thus, the respective values of $a, b$, and $c$ are $-2,-\frac{16}{3}$, and $2 .$