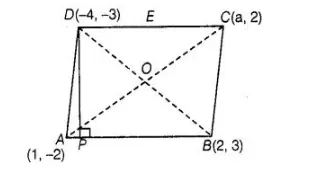
If the points A (1, – 2), B (2, 3), C(a, 2)

In parallelogram, we know that, diagonals are bisects each other i.e., mid-point of AC = mid-point of BD

$\Rightarrow$ $\left(\frac{1+a}{2}, \frac{-2+2}{2}\right)=\left(\frac{2-4}{2}, \frac{3-3}{2}\right)$

$\Rightarrow$ $\frac{1+a}{2}=\frac{2-4}{2}=\frac{-2}{2}=-1$

$\left[\right.$ since, mid-point of a line segment having points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$ is $\left.\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\right]$

$\Rightarrow \quad 1+a=-2$

$\Rightarrow \quad a=-3$

So, the required value of a is – 3.

Given that, AS as base of a parallelogram and drawn a perpendicular from D to AS which meet AS at P. So, DP is a height of a parallelogram.

Now, equation of base $A B$, passing through the points $(1,-2)$ and $(2,3)$ is

$\Rightarrow$ $\left(y-y_{1}\right)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{1}\right)$

$\Rightarrow$ $(y+2)=\frac{3+2}{2-1}(x-1)$

$\Rightarrow$ $(y+2)=5(x-1)$

$\Rightarrow \quad 5 x-y=7$ ....(i)

Slope of $A B$, say $m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3+2}{2-1}=5$

Let the slope of $D P$ be $m_{2}$.

Since, $D P$ is perpendicular to $A B$.

By condition of perpendicularity,

$m_{1} \cdot m_{2}=-1 \Rightarrow 5 \cdot m_{2}=-1$

$\Rightarrow$ $m_{2}=-\frac{1}{5}$

Now, Eq. of $D P$, having slope $\left(-\frac{1}{5}\right)$ and passing the point $(-4,-3)$ is

$\left(y-y_{1}\right)=m_{2}\left(x-x_{1}\right)$

$\Rightarrow \quad(y+3)=-\frac{1}{5}(x+4)$

$\Rightarrow$ $5 y+15=-x-4$

$\Rightarrow$ $x+5 y=-19$ ....(ii)

On adding Eqs. (i) and (ii), then we get the intersection point $P$.

Put the value of $y$ from Eq. (i) in Eq. (ii), we get

$x+5(5 x-7)=-19 \quad$ [using Eq. (i)]

$\Rightarrow \quad x+25 x-35=-19$

$\Rightarrow \quad 26 x=16$

$\therefore$ $x=\frac{8}{13}$

Put the value of $x$ in Eq. (i), we get

$\Rightarrow$ $y=\frac{40-91}{13} \Rightarrow y=\frac{-51}{13}$

$\therefore$ Coordinates of point $P=\left(\frac{8}{13}, \frac{-51}{13}\right)$

So, length of the height of a parallelogram,

$D P=\sqrt{\left(\frac{8}{13}+4\right)^{2}+\left(\frac{-51}{13}+3\right)^{2}}$

$\left[\because\right.$ by distance formula, distance between two points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$, is $\left.d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\right]$

$\Rightarrow$ $D P=\sqrt{\left(\frac{60}{13}\right)^{2}+\left(\frac{-12}{13}\right)^{2}}$

$=\frac{1}{13} \sqrt{3600+144}$

$=\frac{1}{13} \sqrt{3744}=\frac{12 \sqrt{26}}{13}$

Hence, the required length of height of a parallelogram is $\frac{12 \sqrt{26}}{13}$.