If the solve the problem

Given : $f(x)=(x-5)^{4}$

$\Rightarrow f^{\prime}(x)=4(x-5)^{3}$

For a local maximum or a local minimum, we must have

$f^{\prime}(x)=0$

$\Rightarrow 4(x-5)^{3}=0$

$\Rightarrow x=5$

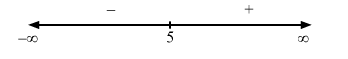
Since $f^{\prime}(x)$ changes from negative to positive when $x$ increases through $5, x=5$ is the point of local minima. The local minimum value of $f(x)$ at $x=5$ is given by

$(5-5)^{4}=0$