If the tangent to the curve

Given:

The Slope of the tangent to the curve $y=x^{3}+a x+b$ at

$(1,-6)$

First, we will find The Slope of tangent

$y=x^{3}+a x+b$

$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{3}\right)+\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{ax})+\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{b})$

$\Rightarrow \frac{d y}{d x}=3 x^{3}-1+a\left(\frac{d x}{d x}\right)+0$

$\Rightarrow \frac{d y}{d x}=3 x^{2}+a$

The Slope of the tangent to the curve $y=x^{3}+a x+b$ at

$(1,-6)$ is

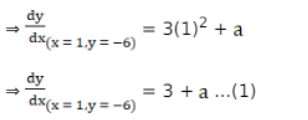
The given line is $x-y+5=0$

$y=x+5$ is the form of equation of a straight line $y=m x+c$, where $m$ is the The Slope of the line.

so the The Slope of the line is $y=1 \times x+5$

so The Slope is $1 \ldots . .(2)$

Also the point $(1,-6)$ lie on the tangent, so

$x=1 \& y=-6$ satisfies the equation, $y=x^{3}+a x+b$

i.e, $-6=1^{3}+a \times 1+b$

$\Rightarrow-6=1+a+b$

$\Rightarrow a+b=-7 \ldots(3)$

Since, the tangent is parallel to the line, from $(1) \&(2)$

Hence,

$3+a=1$

$\Rightarrow a=-2$

From (3)

$a+b=-7$

$\Rightarrow-2+b=-7$

$\Rightarrow b=-5$

$a+b=-7$

$\Rightarrow-2+b=-7$

$\Rightarrow b=-5$

So the value is $a=-2 \& b=-5$