If the volume of parallelopiped formed by the vectors $\hat{\mathrm{i}}+\lambda \hat{\mathrm{j}}+\hat{\mathrm{k}}, \hat{\mathrm{j}}+\lambda \hat{\mathrm{k}}$ and $\lambda \hat{\mathrm{i}}+\hat{\mathrm{k}}$ is minimum, then $\lambda$ is equal to :
Correct Option: , 3
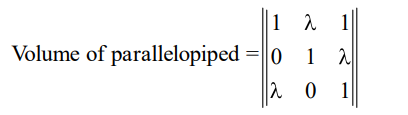
$f(\lambda)=\left|\lambda^{3}-\lambda+1\right|$
Its graph as follows
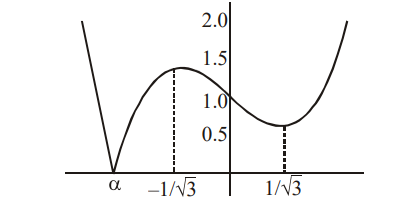
where $\alpha \approx-1.32$
$\because \quad$ Question is asking minimum value of volume of parallelopiped \& corresponding value of $\lambda ;$ the minimum value is zero, $\because$ cubic always has atleast one real root.
Hence answer to the question must be root of cubic $\lambda^{3}-\lambda+1=0$. None of the options satisfies the cubic.
Hence Question must be Bonus.
In JEE (Screening) 2003 same Question was asked and answer was given to be none of these, where the options were :
(A) $-3$
(B) 3
(C) $\frac{1}{\sqrt{3}}$
(D) none of these
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
