If x – √5 is a factor of the cubic polynomial

Let f(x) = x3 – 3√5x2 + 13x – 3√5 and given that, (x – √5) is a one of the factor of f(x). Now, using division algorithm,

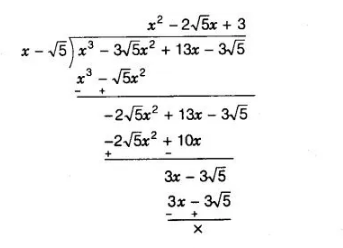
$\therefore \quad x^{3}-3 \sqrt{5} x^{2}+13 x-3 \sqrt{5}=\left(x^{2}-2 \sqrt{5} x+3\right) \times(x-\sqrt{5})$

$[\because$ dividend $=$ divisor $\times$ quotient $+$ remainder $]$

$=(x-\sqrt{5})\left[x^{2}-\{(\sqrt{5}+\sqrt{2})+(\sqrt{5}-\sqrt{2})\} x+3\right] \quad$ [by splitting the middle term]

$=(x-\sqrt{5})\left[x^{2}-(\sqrt{5}+\sqrt{2}) x-(\sqrt{5}-\sqrt{2}) x+(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})\right]$ 

$[\because 3=(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})]$

$=(x-\sqrt{5})[x\{x-(\sqrt{5}+\sqrt{2})\}-(\sqrt{5}-\sqrt{2})\{x-(\sqrt{5}+\sqrt{2})\}]$

$=(x-\sqrt{5})\{x-(\sqrt{5}+\sqrt{2})\}\{x-(\sqrt{5}-\sqrt{2})\}$

Hence, all the zeroes of polynomial are $\sqrt{5},(\sqrt{5}+\sqrt{2})$ and $(\sqrt{5}-\sqrt{2})$.