Question.
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
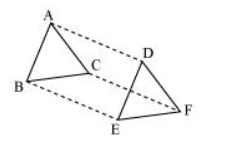
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) $A D \| C F$ and $A D=C F$
(iv) Quadrilateral ACFD is a parallelogram
(v) $\mathrm{AC}=\mathrm{DF}$
(vi) $\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}$

(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) $A D \| C F$ and $A D=C F$
(iv) Quadrilateral ACFD is a parallelogram
(v) $\mathrm{AC}=\mathrm{DF}$
(vi) $\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}$
Solution:
(i) It is given that $A B=D E$ and $A B \| D E$.
If two opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.
Therefore, quadrilateral $\mathrm{ABED}$ is a parallelogram.
(ii) Again, BC = EF and BC || EF
Therefore, quadrilateral BCEF is a parallelogram.
(iii) As we had observed that ABED and BEFC are parallelograms, therefore
$A D=B E$ and $A D \| B E$
(Opposite sides of a parallelogram are equal and parallel)
And, $B E=C F$ and $B E \| C F$
(Opposite sides of a parallelogram are equal and parallel)
$\therefore \mathrm{AD}=\mathrm{CF}$ and $\mathrm{AD} \| \mathrm{CF}$
(iv) As we had observed that one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and parallel to each other, therefore, it is a parallelogram.
(v) As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other.
$\therefore \mathrm{AC} \| \mathrm{DF}$ and $\mathrm{AC}=\mathrm{DF}$
(vi) $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DEF}$,
$\mathrm{AB}=\mathrm{DE}$ (Given)
$\mathrm{BC}=\mathrm{EF}$ (Given)
$\mathrm{AC}=\mathrm{DF}(\mathrm{ACFD}$ is a parallelogram $)$
$\therefore \triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}(\mathrm{By} S S S$ congruence rule $)$
(i) It is given that $A B=D E$ and $A B \| D E$.
If two opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.
Therefore, quadrilateral $\mathrm{ABED}$ is a parallelogram.
(ii) Again, BC = EF and BC || EF
Therefore, quadrilateral BCEF is a parallelogram.
(iii) As we had observed that ABED and BEFC are parallelograms, therefore
$A D=B E$ and $A D \| B E$
(Opposite sides of a parallelogram are equal and parallel)
And, $B E=C F$ and $B E \| C F$
(Opposite sides of a parallelogram are equal and parallel)
$\therefore \mathrm{AD}=\mathrm{CF}$ and $\mathrm{AD} \| \mathrm{CF}$
(iv) As we had observed that one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and parallel to each other, therefore, it is a parallelogram.
(v) As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other.
$\therefore \mathrm{AC} \| \mathrm{DF}$ and $\mathrm{AC}=\mathrm{DF}$
(vi) $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DEF}$,
$\mathrm{AB}=\mathrm{DE}$ (Given)
$\mathrm{BC}=\mathrm{EF}$ (Given)
$\mathrm{AC}=\mathrm{DF}(\mathrm{ACFD}$ is a parallelogram $)$
$\therefore \triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}(\mathrm{By} S S S$ congruence rule $)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
