In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =

Given: In $\triangle \mathrm{ABC} \angle \mathrm{A}=90^{\circ}, \mathrm{AD} \perp \mathrm{BC}, \mathrm{AC}=12 \mathrm{~cm}$, and $\mathrm{AB}=5 \mathrm{~cm}$.

To find: AD

We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

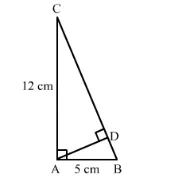
In ∆ACB and ∆ADC,

∠C=∠C        (Common)

∠A=∠ADC=90°  

∴ ∆ACB ~∆ADC     (AA Similarity)

$\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AC}}{\mathrm{BC}}$

$\mathrm{AD}=\frac{\mathrm{AB} \times \mathrm{AC}}{\mathrm{BC}}$

$\mathrm{AD}=\frac{12 \times 5}{13}$

$\mathrm{AD}=\frac{60}{13}$

We got the result as (b)