Question:
In a △ABC, it is given that AD is the internal bisector of ∠A. If AB = 10 cm, AC = 14 cm and BC = 6 cm, the CD = ?
(a) 4.8 cm
(b) 3.5 cm
(c) 7 cm
(d) 10.5 cm
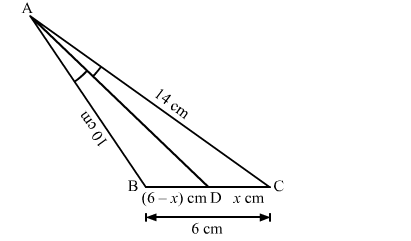
Solution:
By using angle bisector theore in △ABC, we have
$\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{DC}}$
$\Rightarrow \frac{10}{14}=\frac{6-x}{x}$
$\Rightarrow 10 x=84-14 x$
$\Rightarrow 24 x=84$
$\Rightarrow x=3.5$
Hence, the correct answer is option (b).
