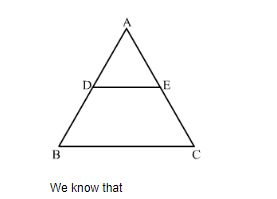
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =

Given: In ΔABC, D is on side AB and point E is on side AC, such that BCED is a trapezium. DE: BC = 3:5.

To find: Calculate the ratio of the areas of ΔADE and the trapezium BCED.

In ΔADE and ΔABC,

∠ADE=∠B           Corresponding angles∠A=∠A                 Common∴∆ADE~∆ABC       AA Similarity

$\frac{\operatorname{Ar}(\Delta \mathrm{ADE})}{\operatorname{Ar}(\Delta \mathrm{ABC})}=\frac{\mathrm{DE}^{2}}{\mathrm{BC}^{2}}$

$\frac{\operatorname{Ar}(\triangle \mathrm{ADE})}{\operatorname{Ar}(\triangle \mathrm{ABC})}=\frac{3^{2}}{5^{2}}$

$\frac{\operatorname{Ar}(\triangle \mathrm{ADE})}{\operatorname{Ar}(\triangle \mathrm{ABC})}=\frac{9}{25}$

Let Area of ΔADE = 9x sq. units and Area of ΔABC = 25x sq. units

$\operatorname{Ar}[\operatorname{trapBCED}]=\operatorname{Ar}(\triangle \mathrm{ABC})-\operatorname{Ar}(\triangle \mathrm{ADE})$

$=25 x-9 x$

$=16 x \mathrm{sq}$ units

Now ,

$\frac{\operatorname{Ar}(\triangle \mathrm{ADE})}{\operatorname{Ar}(\operatorname{trapBCED})}=\frac{9 x}{16 x}$

$\frac{\operatorname{Ar}(\triangle \mathrm{ADE})}{\operatorname{Ar}(\operatorname{trapBCED})}=\frac{9}{16}$

Hence the correct answer is $(b)$.