In a class of a certain school, 50 students, offered mathematics

Given:

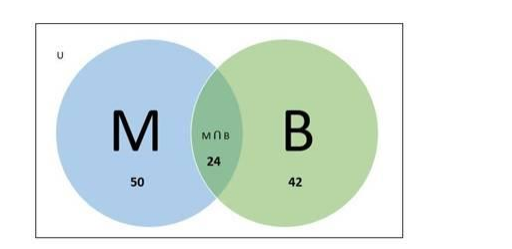
Number of students offered Mathematics $=50$

Number of students offered Biology $=42$

Number of students offered both Mathematics and Biology $=24$

To Find:

(i) Number of students offered Mathematics only

Let us consider,

Number of students offered Mathematics $=n(M)=50$

Number of students offered Biology $=n(B)=42$

Number of students offered Mathematics \& Biology both $=n(M \cap B)=24$

Number of students offered Mathematics only $=n(M-B)$

Venn diagram:

Now

$n(M-B)=n(M)-n(M \cap B)$

$=50-24$

$=26$

Therefore, Number of students offered Mathematics only= 26

(ii) Number of students offered Biology only

Number of students offered Biology only $=n(B-M)$

Now,

$n(B-M)=n(B)-n(M \cap B)$

$=42-24$

$=18$

Therefore, Number of students offered Biology only $=18$

(iii) Number of students offered any of two subjects

Number of students offered any of two subjects $=n(M \cup B)$

Now,

$n(M \cup B)=n(M)+n(B)-n(M \cap B)$

$=50+42-24$

$=140$

Therefore, Number of students offered any of two subjects = 68