In a figure the common tangents,

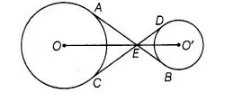
Joint $A O, O C$ and $O^{\prime} D, O^{\prime} B$.

Now, in $\triangle E O^{\prime} D$ and $\triangle E O^{\prime} B$,

$O^{\prime} D=O^{\prime} B$ [radius]

$O^{\prime} E=O^{\prime} E$ [common side]

$E D=E B$

[since, tangents drawn from an external point to the circle are equal in length]

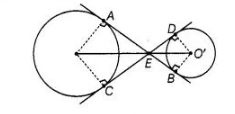
$\therefore$ $\triangle E O^{\prime} D \cong \triangle E O^{\prime} B$ [by SSS congruence ruie]

$\Rightarrow$ $\angle O^{\prime} E D=\angle O^{\prime} E B$ $\ldots$ (i)

$O^{\prime} E$ is the angle bisector of $\angle D E B$.

Similarly, $O E$ is the angle bisector of $\angle A E C$.

Now, in quadrilateral $D E B O^{\prime}$,

$\angle O^{\prime} D E=\angle O^{\prime} B E=90^{\circ}$

[since, $C E D$ is a tangent to the circle and $O^{\prime} D$ is the radius, $i, \theta, O^{\prime} D \perp C E D$ ]

$\Rightarrow \quad \angle O^{\prime} D E+\angle O^{\prime} B E=180^{\circ}$

$\therefore \quad \angle D E B+\angle D O^{\prime} B=180^{\circ} \quad$ [since, $D E B O^{\prime}$ is cyclic quadrilateral] ...(ii)

Since, $A B$ is a straight line.

$\therefore \quad \angle A E D+\angle D E B=180^{\circ}$

$\Rightarrow \quad \angle A E D+180^{\circ}-\angle D O^{\prime} B=180^{\circ} \quad$ [from Eq. (ii)]

$\Rightarrow \quad \angle A E D=\angle D O^{\prime} B$ .....(iii)

Similarly, $\angle A E D=\angle A O C$ ...(iv)

Again from Eq. (ii), $\quad \angle D E B=180^{\circ}-\angle D O^{\prime} B$

Divided by 2 on both sides, we get 

$\frac{1}{2} \angle D E B=90^{\circ}-\frac{1}{2} \angle D O^{\prime} B$

Divided by 2 on both sides, we get

$\frac{1}{2} \angle D E B=90^{\circ}-\frac{1}{2} \angle D O^{\prime} B$

$\Rightarrow$  $\angle D E O^{\prime}=90^{\circ}-\frac{1}{2} \angle D O^{\prime} B$   ....$(\mathrm{v})$

[since, $O^{\prime} E$ is the angle bisector of $\angle D E B i . e, \frac{1}{2} \angle D E B=\angle D E O$ ]

Similarly, $\angle A E C=180^{\circ}-\angle A O C$

Divided bv 2 on both sides, we get

$\frac{1}{2} \angle A E C=90^{\circ}-\frac{1}{2} \angle A O C$

$\Rightarrow$ $\angle A E O=90^{\circ}-\frac{1}{2} \angle A O C$ ....(vi)

[since, $O E$ is the angle bisector of $\angle A E C$ i.e., $\frac{1}{2} \angle A E C=\angle A E O$ ]

Now, $\angle A E D+\angle D E O^{\prime}+\angle A E O=\angle A E D+\left(90^{\circ}-\frac{1}{2} \angle D O^{\prime} B\right)+\left(90^{\circ}-\frac{1}{2} \angle A O C\right)$

$=\angle A E D+180^{\circ}-\frac{1}{2}\left(\angle D O^{\prime} B+\angle A O C\right)$

$=\angle A E D+180^{\circ}-\frac{1}{2}(\angle A E D+\angle A E D)$ [from Eqs. (iii) and (iv)]

$=\angle A E D+180^{\circ}-\frac{1}{2}(2 \times \angle A E D)$

$=\angle A E D+180^{\circ}-\angle A E D=180^{\circ}$

$\therefore \quad \angle A E O+\angle A E D+\angle D E O^{\prime}=180^{\circ}$

So, OEO' is straight line.

Hence, $O, E$ and $O^{\prime}$ are collinear.