Question:
In a $\| \mathrm{gm} A B C D$, if $P$ and $Q$ are midpoints of $A B$ and $C D$ respectively and $\operatorname{ar}(\| \operatorname{gm} A B C D)=16 \mathrm{~cm}^{2}$, then $\operatorname{ar}(\| \operatorname{gm} A P Q D)=?$
(a) $8 \mathrm{~cm}^{2}$
(b) $12 \mathrm{~cm}^{2}$
(c) $6 \mathrm{~cm}^{2}$
(d) $9 \mathrm{~cm}^{2}$
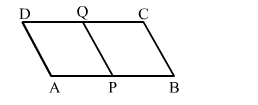
Solution:
(a) $8 \mathrm{~cm}^{2}$
Let the distance between AB and CD be h cm.
Then ar(||gm APQD) = AP × h
$=\frac{1}{2} \times A B \times h \quad\left(\mathrm{AP}=\frac{1}{2} A B\right)$
$=\frac{1}{2} \times \operatorname{ar}(\| \operatorname{gm} A B C D)$ [ ar(|| gm ABCD) = AB ×h )
$\therefore \operatorname{ar}(\| g m A P Q D)=\frac{1}{2} \times 16=8 \mathrm{~cm}^{2}$
