Question:
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
Solution:
Given, a parallelogram ABCD in which AB = 10 cm and AD = 6 cm.
Now, draw a bisector of ∠A meets DC in E and produce it to F and produce BC to meet at F.
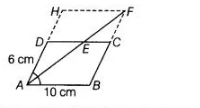
Also, produce $A D$ to $H$ and join $H F$, so that $A B F H$, is a parallelogram.
Since, $H F \| A B$
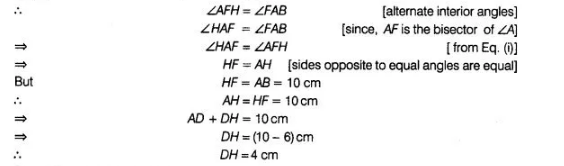
Since, CFHD is a parallelogram.
Therefore, opposite sides are equal.
$\therefore \quad D H=C F=4 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
