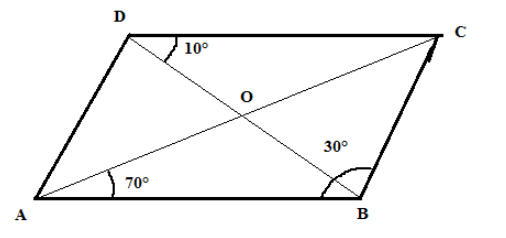
In a parallelogram ABCD, the diagonals bisect each other at O.

$\angle A B C=30^{\circ}$

$\therefore \angle A D C=30^{\circ}$ (opposite angle of the parallelogram)

and $\angle B D A=\angle \mathrm{ADC}-\angle \mathrm{BDC}=30^{\circ}-10^{\circ}=20^{\circ}$

$\angle B A C=\angle A C D=70^{\circ}$ (alternate angle)

In $\triangle \mathrm{ABC}:$

$\angle \mathrm{CAB}+\angle \mathrm{ABC}+\angle \mathrm{BCA}=180^{\circ}$

$70^{\circ}+30^{\circ}+\angle \mathrm{BCA}=180^{\circ}$

$\therefore \angle \mathrm{BCA}=80^{\circ}$

$\angle \mathrm{DAB}=\angle \mathrm{DAC}+\angle \mathrm{CAB}=70^{\circ}+80^{\circ}=150^{\circ}$

$\angle \mathrm{BCD}=150^{\circ}$ (opposite angle of the parallelogram)

$\angle \mathrm{DCA}=\angle C A B=70^{\circ}$

In $\triangle \mathrm{DOC}:$

$\angle \mathrm{ODC}+\angle \mathrm{DOC}+\angle \mathrm{OCD}=180$

$10^{\circ}+70^{\circ}+\angle \mathrm{DOC}=180^{\circ}$

$\therefore \angle \mathrm{DOC}=100^{\circ}$

$\angle \mathrm{DOC}+\angle \mathrm{BOC}=180^{\circ}$

$\angle \mathrm{BOC}=180^{\circ}-100^{\circ}$

$\angle \mathrm{BOC}=80^{\circ}$

$\angle A O D=\angle B O C=80^{\circ} \quad$ (vertically opposite angles)

$\angle \mathrm{AOB}=\angle \mathrm{DOC}=100^{\circ} \quad$ (vertically opposite angles)

$\angle \mathrm{CAB}=70^{\circ}$ (given)

$\angle \mathrm{ADB}=20^{\circ}$

$\angle D B A=\angle B D C=10^{\circ} \quad$ (alternate angle)

$\angle A D B=\angle D B C=20^{\circ} \quad$ (alternate angle)