Question:
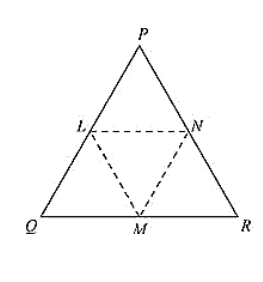
In a Δ PQR. IF PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN = MN.
Solution:
Given that in ΔPQR, PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP respectively
We have to prove LN = MN.
Join L and M, M and N, N and L
We have PL = LQ, QM = MR and RN = NP
[Since, L, M and N are mid-points of Pp. QR and RP respectively]
And also PQ = QR
PL = LQ = QM = MR = PQ/2 = QR/2 ... (i) Using mid-point theorem,
We have
MN ∥ PQ and MN = PQ/2
MN = PL = LQ ... (ii)
Similarly, we have
LN ∥ QR and LN = (1/2)QR
LN = QM = MR ... (iii)
From equation (i), (ii) and (iii), we have
PL = LQ = QM = MR = MN = LN
LN = MN
