In a quadrilateral ABCD, given that ∠A + ∠D = 90°.

Given: A quadrilateral $\mathrm{ABCD}$ where $\angle \mathrm{A}+\angle \mathrm{D}=90^{\circ}$.

To prove: $\mathrm{AC}^{2}+\mathrm{BD}^{2}=\mathrm{AD}^{2}+\mathrm{BC}^{2}$

Construction: Extend AB and CD to intersect at O.

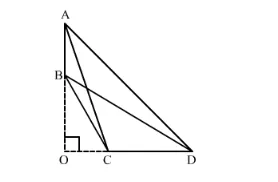
Proof:

In $\triangle \mathrm{AOD}, \angle \mathrm{A}+\angle \mathrm{O}+\angle \mathrm{D}=180^{\circ}$

$\Rightarrow \angle O=90^{\circ}\left[\angle A+\angle D=90^{\circ}\right]$

Apply Pythagoras Theorem in $\triangle A O C$ and $\triangle B O D$,

$\mathrm{AC}^{2}=\mathrm{AO}^{2}+\mathrm{OC}^{2}$

$\mathrm{BD}^{2}=\mathrm{OB}^{2}+\mathrm{OD}^{2}$

$\therefore \mathrm{AC}^{2}+\mathrm{BD}^{2}=\left(\mathrm{AO}^{2}+\mathrm{OD}^{2}\right)+\left(\mathrm{OC}^{2}+\mathrm{OB}^{2}\right)$

$\Rightarrow \mathrm{AC}^{2}+\mathrm{BD}^{2}=\mathrm{AD}^{2}+\mathrm{BC}^{2}$

This proves the given relation.