In a quadrilateral ΔBCD, ∠A+ ∠D = 90°.

Given Quadrilateral ΔBCD, in which ∠A+ ∠D = 90°

To prove                                  AC2 + BD2 = AD2 + BC2

Construct Produce AB and CD to meet at E.

Also, join $A C$ and $B D$.

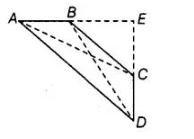
Proof In $\triangle A E D, \quad \angle A+\angle D=90^{\circ}$ [given]

$\therefore$ $\angle E=180^{\circ}-(\angle A+\angle D)=90^{\circ}$

Then, by Pythagoras theorem, $\quad A D^{2}=A E^{2}+D E^{2}$

In $\triangle B E C$, by Pythagoras theorem, $B C^{2}=B E^{2}+E F^{2}$

On adding both equations, we get

$A D^{2}+B C^{2}=A E^{2}+D E^{2}+B E^{2}+C E^{2}$ ...(i)

In $\triangle A E C$, by Pythagoras theorem,

$A C^{2}=A E^{2}+C E^{2}$

and in $\triangle B E D$, by Pythagoras theorem,

$B D^{2}=B E^{2}+D E^{2}$

On adding both equations, we get

$A C^{2}+B D^{2}=A E^{2}+C E^{2}+B E^{2}+D E^{2}$  ......(ii)

From Eqs. (i) and (ii), 

$A C^{2}+B D^{2}=A D^{2}+B C^{2}$

Hence proved.