In a right triangle ABC, right angled at C,

We are given the following triangle with related information

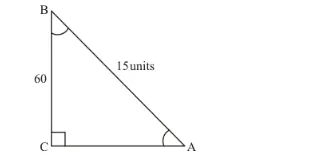
It is required to find $\angle A, \angle C$ and length of sides $A C$ and $B C$

$\triangle A B C$ is right angled at $C$

Therefore,

$\angle C=90^{\circ}$

Now we know that sum of all the angles of any triangle is $180^{\circ}$

Therefore,

$\angle A+\angle B+\angle C=180^{\circ}$.....(1)

Now by substituting the values of known angles $\angle B$ and $\angle C$ in equation (1)

We get,

$\angle A+60^{\circ}+90^{\circ}=180^{\circ}$

Therefore,

$\angle A+150^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle A=180^{\circ}-150^{\circ}$

$\Rightarrow \quad \angle A=30^{\circ}$

Therefore,

$\angle A=30^{\circ}$

Now,

We know that,

$\cos B=\cos 60^{\circ}$

$\Rightarrow \quad \frac{B C}{A B}=\cos 60^{\circ}$....(2)

Now we have,

$A B=15$ units and $\cos 60^{\circ}=\frac{1}{2}$

Therefore by substituting above values in equation (2)

We get,

$\cos B=\cos 60^{\circ}$

$\Rightarrow \quad \frac{B C}{A B}=\cos 60^{\circ}$

$\Rightarrow \frac{B C}{15}=\frac{1}{2}$

Now by cross multiplying we get,

$\frac{B C}{15}=\frac{1}{2}$

$\Rightarrow 2 \times B C=15 \times 1$

$\Rightarrow \quad B C=\frac{15}{2}$

$\Rightarrow \quad B C=7.5$

Therefore,

$B C=7.5$ units.....(3)

Now,

We know that,

$\sin B=\sin 60^{\circ}$

$\Rightarrow \frac{A C}{A B}=\sin 60^{\circ}$........(4)

Now we have,

$A B=15$ units and $\sin 60^{\circ}=\frac{\sqrt{3}}{2}$

Therefore by substituting above values in equation (4)

We get,

$\sin B=\sin 60^{\circ}$

$\Rightarrow \frac{A C}{A B}=\sin 60^{\circ}$

$\Rightarrow \frac{A C}{15}=\frac{\sqrt{3}}{2}$

Now by cross multiplying we get,

$\frac{A C}{15}=\frac{\sqrt{3}}{2}$

$\Rightarrow 2 \times A C=\sqrt{3} \times 15$

$\Rightarrow \quad A C=\frac{\sqrt{3} \times 15}{2}$

$\Rightarrow \quad A C=\frac{15}{2} \sqrt{3}$

Therefore,

$A C=\frac{15}{2} \sqrt{3}$ units

Hence,

$\angle A=30^{\circ}$

$B C=7.5$ units

$A C=\frac{15}{2} \sqrt{3}$ units