In a survey of 100 students, the number of students studying the various

Given:

- Total number of students $=100$

- Number of students studying English(E) only $=18$

- Number of students learning English but not Hindi(H) $=23$

- Number of students learning English and Sanskrit(S) $=8$

- Number of students learning Sanskrit and Hindi = 8

- Number of students learning English = 26

- Number of students learning Sanskrit = 48

- Number of students learning no language $=24$

To Find:

(i) Number of students studying Hindi

Venn diagram:

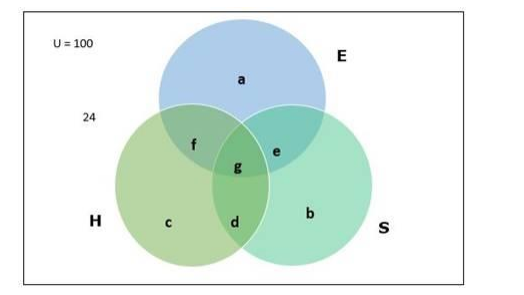
From the above Venn diagram

$\mathrm{a}=$ Number of students who study only English $=18$

$\mathrm{~b}=$ Number of students who study only Sanskrit

$\mathrm{c}=$ Number of students who study only Hindi

$\mathrm{d}=$ Number of students learning Hindi and Sanskrit but not English

$\mathrm{e}=$ Number of students learning English and Sanskrit but not Hindi

$\mathrm{f}=$ Number of students learning Hindi and English but not Sanskrit

$\mathrm{g}=$ Number of students learning all the three languages

$\mathrm{e}+\mathrm{g}=$ Number of students learning English and Sanskrit $=8$

$=n(E \cap S)$

g + d = Number of students learning Hindi and Sanskrit = 8

$=n(H \cap S)$

$E=a+e+f+g=$ Number of students learning English $26=18+8+f$

$f=26-26=0$

Therefore, $f=0$

Now

Number of students learning English but not Hindi = a + e = 23

$23=18+e$

Therefore, $e=5$

Now, $e+g=8$

$5+g=8$

Therefore, $g=3$

$S=b+e+d+g=$ Number of students studying Sanskrit

$48=b+5+8$ (Because, $d+g=8$ )

$b=48-13$

Therefore, $b=35$ (Number of students studying Sanskrit only)

Also, $d+g=8$

$d+3=8$

Therefore, $d=5$

Now,

Number of students studying Hindi only $=c$

$c=100-(a+e+b+d+f+g)-24$

$=100-(18+5+35+5+0+3)-24$

$=100-66-24$

$=100-90=10$

Number of students studying Hindi $=c+f+g+d$

$=10+0+3+5$

$=18$

Therefore, number of students studying Hindi $=18$

(ii) Number of students studying English and Hindi both

Number of students studying English and Hindi both $=f+g$

$=0+3=3$

Therefore, Number of students studying English and Hindi both = 3