In a survey of 60 people, it was found that 25 people read newspaper

Given:

- Total number of people $=60$

- Number of people who read newspaper $\mathrm{H}=25$

- Number of people who read newspaper $\mathrm{T}=26$

- Number of people who read newspaper $I=26$

- Number of people who read newspaper $\mathrm{H}$ and $\mathrm{I}$ both $=9$

- Number of people who read newspaper $\mathrm{H}$ and $\mathrm{T}$ both $=11$

- Number of people who read newspaper $T$ and $I$ both $=8$

- Number of people who read all three newspapers $=3$

To Find:

(i) The number of people who read at least one of the newspapers

Let us consider,

Number of people who read newspaper $\mathrm{H}=\mathrm{n}(\mathrm{H})=25$

Number of people who read newspaper $\mathrm{T}=\mathrm{n}(\mathrm{T})=26$

Number of people who read newspaper $I=n(I)=26$

Number of people who read newspaper $\mathrm{H}$ and $\mathrm{I}$ both $=\mathrm{n}(\mathrm{H} \cap \mathrm{I})=9$

Number of people who read newspaper $\mathrm{H}$ and $\mathrm{T}$ both $=\mathrm{n}(\mathrm{H} \cap \mathrm{T})=11$

Number of people who read newspaper $T$ and $I$ both $=n(T \cap I)=8$

Number of people who read all three newspapers $=\mathrm{n}(\mathrm{H} \cap \mathrm{T} \cap \mathrm{I})=3$

Number of people who read at least one of the three newspapers $=n(H U$ U U I)

Venn diagram:

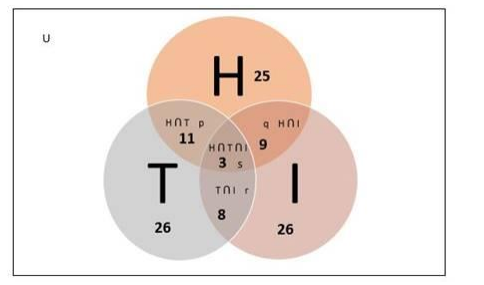
We know that,

$n(H U T U I)=n(H)+n(T)+n(I)-n(H \cap I)-n(H \cap T)-n(T \cap I)+n(H \cap T \cap I)$

$=25+26+26-9-11-8+3$

$=52$

Therefore

Number of people who read at least one of the three newspapers = 52

(ii) The number of people who read exactly one newspaper

Number of people who read exactly one newspaper =

$\mathrm{n}(\mathrm{HU} \mathrm{U} \mathrm{U} \mathrm{l})-\mathrm{p}-\mathrm{q}-\mathrm{r}-\mathrm{s}$

Where,

$p=$ Number of people who read newspaper $H$ and $T$ but not $I$

$q=$ Number of people who read newspaper $H$ and $I$ but not $T$

$r=$ Number of people who read newspaper $T$ and $I$ but not $H$

$s=$ Number of people who read all three newspapers $=3$

$p+s=n(H \cap T) \ldots(1)$

$q+s=n(H \cap I) \ldots(2)$

$r+s=n(T \cap I) \ldots(3)$

Adding $(1),(2)$ and $(3)$

$p+s+q+s+r+s=n(H \cap T)+n(H \cap I)+n(T \cap I)$

$p+q+r+3 s=9+11+8$

$p+q+r+s+2 s=28$

$p+q+r+s=28-2 \times 3$

$p+q+r+s=22$

Now,

$n(H U \top U I)-p-q-r-s=n(H U T U I)-(p+q+r+s)$

$=52-22$

$=30$

Hence, 30 people read exactly one newspaper