In a survey of 60 people, it was found that 25 people read newspaper H,

Let A be the set of people who read newspaper H.

Let B be the set of people who read newspaper T.

Let C be the set of people who read newspaper I.

Accordingly, $n(A)=25, n(B)=26$, and $n(C)=26$

$n(\mathrm{~A} \cap \mathrm{C})=9, n(\mathrm{~A} \cap \mathrm{B})=11$, and $n(\mathrm{~B} \cap \mathrm{C})=8$

$n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})=3$

Let $U$ be the set of people who took part in the survey.

(i) Accordingly,

$n(\mathrm{~A} \cup \mathrm{B} \cup \mathrm{C})=n(\mathrm{~A})+n(\mathrm{~B})+n(\mathrm{C})-n(\mathrm{~A} \cap \mathrm{B})-n(\mathrm{~B} \cap \mathrm{C})-n(\mathrm{C} \cap \mathrm{A})+n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})$

= 25 + 26 + 26 – 11 – 8 – 9 + 3

= 52

Hence, 52 people read at least one of the newspapers.

(ii) Let a be the number of people who read newspapers H and T only.

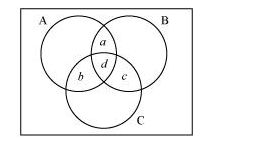
Let b denote the number of people who read newspapers I and H only.

Let c denote the number of people who read newspapers T and I only.

Let d denote the number of people who read all three newspapers.

Accordingly, $d=n(\mathrm{~A} \cap \mathrm{B} \cap \mathrm{C})=3$

Now, $n(\mathrm{~A} \cap \mathrm{B})=a+d$

$n(B \cap C)=c+d$

$n(\mathrm{C} \cap \mathrm{A})=b+d$

$\therefore a+d+c+d+b+d=11+8+9=28$

$\Rightarrow a+b+c+d=28-2 d=28-6=22$

Hence, $(52-22)=30$ people read exactly one newspaper.