In a town of 10,000 families, it was found that 40% of the families buy

Given:

Total number of families $=10000$

Percentage of families that buy newspaper $A=40$

Percentage of families that buy newspaper $B=20$

Percentage of families that buy newspaper $C=10$

Percentage of families that buy newspaper $A$ and $B=5$

Percentage of families that buy newspaper $B$ and $C=3$

Percentage of families that buy newspaper $A$ and $C=4$

Percentage of families that buy all three newspapers $=2$

To find:

(i) Number of families that buy newspaper A only

Consider the Venn Diagram below

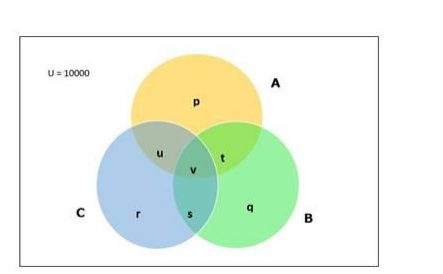
Number of families that buy newspaper A = n(A) = 40% of 10000

= 4000

Number of families that buy newspaper B = n(B) = 20% of 10000 = 2000

Number of families that buy newspaper C = n(C) = 10% of 10000

= 1000

Number of families that buy newspaper $A$ and $B=n(A \cap B)$

$=5 \%$ of 10000

$=500$

Number of families that buy newspaper $B$ and $C=n(B \cap C)$

$=3 \%$ of 10000

$=300$

Number of families that buy newspaper $A$ and $C=n(A \cap C)$

$=4 \%$ of 10000

$=400$

Number of families that buys all three newspapers $=n(A \cap B \cap C)=v$

$=2 \%$ of 10000

$=200$

We have,

$n(A \cap B)=v+t$

$500=200+t$

$\mathrm{t}=500-200=300$

$\mathrm{n}(\mathrm{B} \cap \mathrm{C})=\mathrm{v}+\mathrm{s}$

$300=200+\mathrm{s}$

$\mathrm{s}=300-200=100$

$\mathrm{n}(\mathrm{A} \cap \mathrm{C})=\mathrm{v}+\mathrm{u}$

$400=200+\mathrm{u}$

$\mathrm{u}=400-200=200$

p = Number of families that buy newspaper A only

We have,

$A=p+t+v+u$

$4000=p+300+200+200$

$p=4000-700$

$p=3300$

Therefore,

Number of families that buy newspaper A only = 3300

(ii) Number of families that buy newspaper B only

q = Number of families that buy newspaper B only

$B=q+s+v+t$

$2000=q+100+200+300$

$q=2000-600=1400$

Therefore,umber of families that buy newspaper B only = 1400

(iii) Number of families that buys none of the newspaper

Number of families that buy none of the newspaper =

$10000-\{n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(A \cap C)+n(A \cap B \cap C)\}$

$=10000-(4000+2000+1000-500-300-400+200)$

$=10000-6000$

$=4000$

Therefore,

Number of families that buy none of the newspaper = 4000