In a town of 6000 people, 1200 are over 50 years old, and 2000 are females.

let A denote the event that the chosen individual is female and B denote the event that the chosen individual is over 50 years old.

Given : Town consists of 6000 people, 1200 are over 50 years old, and 2000 are females

To find : Probability that a randomly chosen individual from the town is either female or over 50 years $=P(A$ or $B)$

The formula used : Probability =

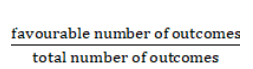
$P(A$ or $B)=P(A)+P(B)-P(A$ and $B)$

For the event $A$,

There are 2000 females present in a town of 6000 people

Favourable number of outcomes $=2000$

Total number of outcomes $=6000$

$P(A)=\frac{2000}{6000}=\frac{1}{3}$

For the event B,

There are 1200 are over 50 years of age in a town of 6000 people

Favourable number of outcomes $=1200$

Total number of outcomes $=6000$

$P(A)=\frac{1200}{6000}=\frac{1}{5}$

$30 \%$ of the females are over 50 years

For the event $A$ and $B$,

$\frac{30}{100} \times 2000=600$

females are over 50 years of age

Favourable number of outcomes = 600

$P(A$ and $B)=\frac{600}{6000}=\frac{1}{10}$

$P(A$ or $B)=P(A)+P(B)-P(A$ and $B)$

$P(A$ or $B)=\frac{1}{3}+\frac{1}{5}-\frac{1}{10}$

$P(A$ or $B)=\frac{10+6-3}{30}=\frac{13}{30}$

$P(A$ or $B)=\frac{13}{30}$

The probability that a randomly chosen individual from the town is either female or over

50 years $=P(A$ or $B)=\frac{13}{30}$