Question:
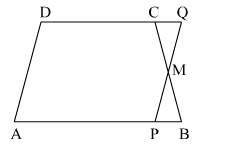
In a trapezium ABCD, AB || DC and M is the midpoint of BC. Through M, a line PQ || AD has been drawn which meets AB in P and DC produced in Q, as shown in the adjoining figure. Prove that ar(ABCD) = ar(APQD).
Solution:
In △MQC and △MPB,
MC = MB (M is the midpoint of BC)
∠CMQ = ∠BMP (Vertically opposite angles)
∠MCQ = ∠MBP (Alternate interior angles on the parallel lines AB and DQ)
Thus, △MQC ≅ △MPB (ASA congruency)
⇒ar(△MQC) = ar(△MPB)
⇒ar(△MQC) + ar(APMCD) = ar(△MPB) + ar(APMCD)
⇒ar(APQD) = ar(ABCD)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.