Question:
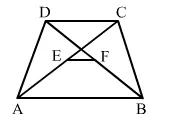
In a trapezium ABCD, if E and F be the mid-point of the diagonals AC and BD respectively. Then, EF = ?
(a) $\frac{1}{2} A B$
(b) $\frac{1}{2} C D$
(c) $\frac{1}{2}(A B+C D)$
(d) $\frac{1}{2}(A B-C D)$
Solution:
(d) $\frac{1}{2}(A B-C D)$
Explanation:
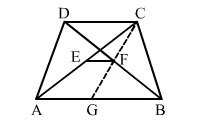
Join CF and produce it to cut AB at G.
Then ∆CDF ≅ ∆GBF [∵ DF = BF, ∠DCF = ∠BGF and ∠CDF = ∠GBF]
∴ CD = GB
Thus, in ∆CAG, the points E and F are the mid points of AC and CG, respectively.
$\therefore E F=\frac{1}{2}(A G)=\frac{1}{2}(A B-G B)=\frac{1}{2}(A B-C D)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.