In a trapezium ABCD, it is given that AB∥CD and AB = 2 CD. Its diagonals AC and BD intersect at a point

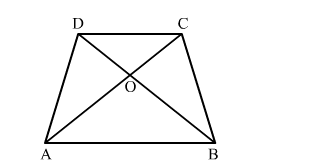
In △AOB and COD
∠ABO = ∠CDO         (Alternte angles in AB∥CD)
∠AOB = ∠COD         (Vertically opposite angles)
By AA similarity criterion, △AOB ∼ △COD
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.

$\therefore \frac{\operatorname{area}(\triangle \mathrm{AOB})}{\operatorname{area}(\triangle \mathrm{COD})}=\left(\frac{\mathrm{AB}}{\mathrm{CD}}\right)^{2}$

$\Rightarrow \frac{84}{\operatorname{area}(\triangle \mathrm{COD})}=\left(\frac{2 \mathrm{CD}}{\mathrm{CD}}\right)^{2}$

$\Rightarrow$ area $(\triangle \mathrm{COD})=12 \mathrm{~cm}^{2}$