In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:

Given: ΔABC where ∠BAC is obtuse. PB ⊥AC and QC⊥AB.

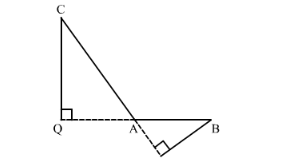
To prove: (i) $\mathrm{AB} \times \mathrm{AQ}=\mathrm{AC} \times \mathrm{AP}$ and (ii) $\mathrm{BC}^{2}=\mathrm{AC} \times \mathrm{CP}+\mathrm{AB} \times \mathrm{BQ}$

Proof: In $\triangle \mathrm{ACQ}$ and $\triangle \mathrm{ABP}$,

$\angle C A Q=\angle B A P($ Vertically opposite angles $)$

$\angle Q=\angle P\left(=90^{\circ}\right)$

$\therefore \triangle \mathrm{ACQ} \sim \triangle \mathrm{ABP}[\mathrm{AA}$ similarity test]

$\Rightarrow \frac{\mathrm{CQ}}{\mathrm{BP}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{AQ}}{\mathrm{AP}}$ [Corresponding sides are in the same proportion]

$\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{AQ}}{\mathrm{AP}}$

$\Rightarrow \mathrm{AQ} \times \mathrm{AB}=\mathrm{AC} \times \mathrm{AP}$.....(1)

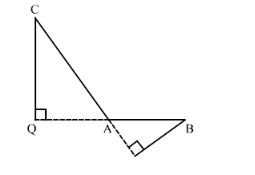
In right $\triangle B C Q$,

$\Rightarrow B C^{2}=C Q^{2}+Q B^{2}$

$\Rightarrow B C^{2}=C Q^{2}+(Q A+A B)^{2}$

$\Rightarrow B C^{2}=C Q^{2}+Q A^{2}+A B^{2}+2 Q A \times A B$

$\Rightarrow B C^{2}=A C^{2}+A B^{2}+Q A \times A B+Q A \times A B$  [In right $\triangle \mathrm{ACQ}, \mathrm{CQ}^{2}+\mathrm{QA}^{2}=\mathrm{AC}^{2}$ ]

$\Rightarrow B C^{2}=A C^{2}+A B^{2}+Q A \times A B+A C \times A P$(Using (1))

$\Rightarrow B C^{2}=A C(A C+A P)+A B(A B+Q A)$

$\Rightarrow B C^{2}=A C \times C P+A B \times B Q$